Pour biaiser le tirage du loto...

Un lecteur, suite à mes messages du 17 et du 21 février sur la fonction alea(), m'a demandé comment faire pour tirer les nombres du loto (de 1 à 49) en favorisant certains numéros et en en défavorisant d’autres.

J'ai pour cela créé un petit modèle avec en colonne B les probabilités voulues, en réduisant celles des premiers numéros et en augmentant celle des derniers numéros. La cellule B51 vérifie que le total des probabilités fait bien 100%.

En colonne C, nous calculons les probabilités cumulées, c’est-à-dire la probabilité dans chaque ligne d’obtenir un résultat inférieur au nombre placé en colonne A.

La formule de la cellule E2, que nous avons reproduite en commentaire, permet de tirer un nombre au hasard entre 1 et 49, en respectant ces probabilités.

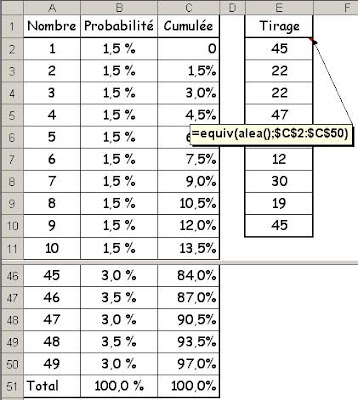L’astuce de cette formule est qu’elle trouve le nombre comme étant la position de la dernière valeur de C2:C50 qui soit inférieure ou égale au nombre aléatoire engendré par alea(). La probabilité de trouver chaque numéro est donc bien égale à la probabilité en colonne B…

Remarque 1 – Bien entendu, rien n’empêche que le même nombre sorte plusieurs fois dans la liste.

Remarque 2 – Tirer ainsi un aléa dans l’intervalle [ 0 ; 1 ] et le situer dans une liste de probabilités cumulées est donc une méthode imparable pour réaliser une simulation probabiliste d'un phénomène dont on connaît les probabilités.

L’utilitaire d’analyse est-il présent ?

Quand on utilise des fonctions de l’utilitaire d’analyse, telle la fonction alea.entre.bornes() présentée dans le dernier message, cela engendre des erreurs si la macro « Utilitaire d’analyse » n’est pas chargée en mémoire. Cela peut gravement troubler des utilisateurs du modèle qui ne seraient pas au courant de l’existence de cet utilitaire.

Il est donc sage – si l’on souhaite rendre un modèle utilisable par tous – que la présence ou non de l’utilitaire soit testée dès l’ouverture du classeur, et qu’un message approprié soit affiché quand l’utilitaire n’est pas en mémoire.

Pour cela, définissons tout d’abord dans le classeur une cellule nommée
« Test », dans laquelle nous entrons une formule requérant la présence de l’utilitaire d’analyse, par exemple =alea.entre.bornes(1;10).

La petite macro ci-dessous – à placer précisément dans ThisWorkbook – résout le problème :

Remarque 1 – Bien évidemment, quand tout va bien, il n’est pas nécessaire de dire que tout va bien : le second message peut donc tout simplement être remplacé par « Exit Sub ». On fera alors encore plus court avec une macro en deux lignes : If Not(Iserror(Range(״Test״))) Then Exit Sub, puis le MsgBox avec le message d’explication.

Remarque 2 – De même, quand il y a un problème, il faudrait idéalement un message plus détaillé expliquant comment il faut s’y prendre pour charger en mémoire la macro « Utilitaire d’analyse ».

Et la fonction alea.entre.bornes() ?

Excel propose aussi une fonction alea.entre.bornes(min;max), qui engendre un nombre aléatoire entier dans l’intervalle [min ; max], mais je vous conseille de ne pas l’utiliser.

En effet, tout d'abord, elle n’est accessible que si la macro complémentaire
« Utilitaire d’analyse », livrée avec Excel, est en mémoire. Si donc l’utilisateur de votre modèle n’a pas cet add-in en mémoire, la formule aboutira au fatidique #VALEUR!

Ensuite, on fait mieux et plus simple avec une formule Excel n’utilisant que la fonction alea().


Remarque 1 – Comme vous le voyez ci-dessus, l’assistant fonction omet de vous indiquer que le nombre aléatoire entre le min et le max est un nombre entier ! En plus, Microsoft ne vous dit évidemment pas ce qui arrive quand les bornes ne sont pas entières…

Remarque 2 – Quand vous cliquez en bas à gauche dans « Aide sur cette fonction », vous obtenez une fenêtre vide (cf. écran ci-dessus). Une fois encore, notons que l’aide d’Excel est franchement à revoir.

En fait, =alea.entre.bornes(a;b) équivaut donc, après les essais que j’ai effectués, à la formule : =arrondi.sup(min;0)+ent((arrondi.inf(max;0)-arrondi.sup(min;0)+1)*alea()).

Si les bornes sont entières et que vous voulez un résultat entier comme la fonction alea.entre.bornes() le calculerait, il vous suffit d’entrer la formule =min+ent((max-min+1)*alea()) !

Utilisation de la fonction alea()

Dans la mesure où j’anime de nombreuses formations, entre mes cours à HEC et les formations dans les entreprises sur les thèmes « Modélisation avec Excel » et « Modélisation du risque », j’utilise fréquemment la fonction alea().

La fonction alea() d’Excel ne comporte aucun argument, mais il faut quand même ne pas oublier ses parenthèses, sinon le résultat #NOM! vous indiquera qu’Excel n’a trouvé aucun nom correspondant à « alea ». Elle engendre un résultat aléatoire dans l’intervalle [0 ; 1[ donc avec le « 1 » exclus, et pris selon une loi uniforme.

Elle est très pratique dans les formations car, comme les valeurs changent à chaque recalcul du classeur, on peut ainsi tester les comportements des formules selon les valeurs obtenues.

Pour trouver un résultat aléatoire continu dans l’intervalle [min ; max[, vous pouvez utiliser la formule =min+(max-min)*alea().

Remarque 1 – Pour tirer les numéros du prochain tirage du loto, utilisez donc la formule =1+ent(49*alea()) et – si vous gagnez – adressez un chèque de 10% de vos gains à une œuvre caritative…

Le modèle ci-dessous réalise un classement au hasard de huit personnes selon les valeurs aléatoires obtenues, par exemple pour organiser l’ordre dans lequel ces personnes pourront choisir un cadeau parmi une liste de cadeaux proposés :

Remarque 2 – Un avantage de la fonction alea() est que la probabilité d’obtenir deux fois la même valeur est quasiment nulle, de l’ordre de 10^-14 ; en effet, un nombre dans Excel a environ 14 chiffres significatifs.

Vive la correction automatique !

Un lecteur m’apprenait récemment qu’il ne parvenait plus dans Excel à obtenir « € » avec la combinaison [Alt Gr]-e, alors que cette combinaison fonctionnait toujours sous Word. Et il me demandait comment restituer la situation normale…

Je ne connais pas la réponse : n’ayant jamais eu ce problème, je ne peux rien tenter pour essayer de le résoudre. Si un lecteur peut nous dire en commentaire à ce message comment cela peut arriver et – mieux encore – quel est le remède, nous en serons ravis.

Faute de mieux, j’ai proposé une solution tout à fait opérationnelle : il suffit de passer par la commande « Options de correction automatique » du menu Outils et d’associer par exemple la touche « € » à la frappe de « $$ », une combinaison qui ne devrait pas apparaître de façon naturelle dans un modèle Excel :

Dès lors, dès que vous taperez « $$ », cela sera remplacé par « € » de façon automatique. La correction automatique n’est pas utile que dans Word ou Powerpoint…

Remarque 1 – Vous allez me dire que vous ne pouvez pas entrer le « € » dans l’écran ci-dessus puisqu’il n’est plus accessible… Ce n’est pas un problème, tapez-le dans Word, copiez-le puis collez-le avec [Ctrl]-v dans le dialogue ci-dessus.

Remarque 2 – Sans passer par Word, vous pouvez aussi obtenir le caractère
« € » dans Excel, même avec la touche [Alt Gr] cassée, en entrant la formule =car(128).

Voici à titre informatif quelques caractères potentiellement intéressants dans Excel que l’on récupère avec la fonction car(). Bien entendu, une fois générés dans Excel, ces caractères peuvent par exemple être intégrés à des formats personnalisés…

Où faut-il mettre vos graphiques ?

Quand on crée un graphique, Excel propose de le loger soit dans une feuille graphique, soit dans la feuille de calcul active.

Pour ma part, je ne vois aucun intérêt à loger un graphique dans une feuille graphique. Voici déjà deux des inconvénients que j’y vois…

Tout d’abord, une feuille graphique ne peut comporter qu’un graphe unique : l’utilisation de feuilles graphiques entraîne donc une augmentation sensible du nombre de feuilles du classeur, ce qui n’a que des conséquences négatives sur la clarté, la taille, ou encore la vitesse de calcul du modèle.

Enfin, l’impression d’un graphe logé sur une feuille graphique immobilise une page entière, ce qui représente un gâchis à la fois en papier et en temps d’impression.

Je crée donc tous mes graphiques dans des feuilles de calcul. Quand je souhaite loger toute une série de graphiques sur la même feuille, j’ancre chaque graphique dans une cellule unique – après avoir bien entendu modifié en conséquence les largeurs de lignes et hauteurs de colonnes – de la feuille de calcul. Si un graphique doit être plus large que les autres, je l’ancre sur deux cellules voisines.

Vous en voyez un exemple ci-dessous avec des graphiques que j’ai réalisés pour le bilan social d’un de mes clients. J’ai seulement modifié certains éléments pour respecter les accords de confidentialité liés à ce contrat.

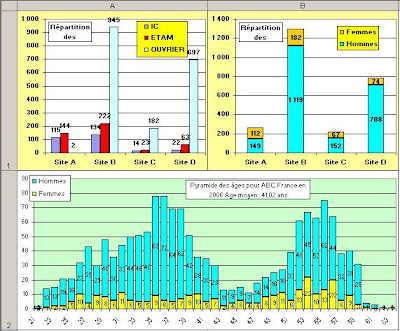Avec cette technique d’ancrage des graphiques dans les cellules, il devient extrêmement facile de modifier d’un coup la largeur et/ou la hauteur de tous les graphiques. Pour cela, on clique dans le coin supérieur gauche de la feuille pour la sélectionner toute entière ; ensuite, on modifie – selon les besoins – la hauteur d’une ligne et/ou la largeur d’une colonne. Toutes les lignes et colonnes prennent alors en compte cette modification.

On adapte ainsi en très peu de temps la totalité des graphiques afin de tirer le meilleur parti possible de l’écran et/ou de l’imprimante dont on dispose…

Déformation d’un objet dans Excel

Les touches que nous avons utilisées lors de notre dernière rubrique, pour le déplacement d’un objet dans Excel, fonctionnent tout aussi bien quand on redimensionne un objet : si l’on maintient la touche [Alt] enfoncée lors du redimensionnement, celui-ci ne s’opère que par rapport aux bordures des cellules concernées.

Remarque – Quand on redimensionne un objet avec la touche [Alt] enfoncée, cet objet est automatiquement ancré sur les cellules à l’intérieur desquelles il est logé.

Vous le vérifiez aisément en faisant un clic droit sur l’objet et en appelant la commande « Format… » associée du menu contextuel, onglet « Propriétés » :

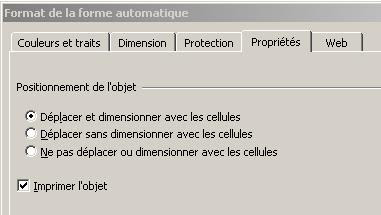« Déplacer et dimensionner avec les cellules » signifie que si l’on modifie la hauteur ou la largeur d’une ligne ou d’une colonne à l’intérieur de l’objet, la taille de l’objet est modifiée de façon qu’il demeure ancré sur les mêmes lignes et colonnes.

Si vous sélectionnez le troisième bouton radio, vous désolidarisez l’objet de la structure lignes & colonnes d’Excel.

Si, lors du redimensionnement de l’objet, vous maintenez la touche [Ctrl] enfoncée, l'objet se déforme en maintenant son centre fixe.

En revanche, et de bien entendu, si vous maintenez la touche [Ctrl] lors du déplacement de l’objet, vous le clonez.

Si en outre vous maintenez aussi la touche [Maj] enfoncée, l’objet cloné reste dans la même ligne ou colonne que l’objet initial, selon la première direction donnée à votre souris (plutôt horizontale ou plutôt verticale).

Si enfin vous maintenez en plus la touche [Alt] enfoncée, l’objet cloné reste dans la même ligne ou colonne que l’objet initial et il se positionne en outre contre des bords de cellule.

C’est en faisant ainsi des clonages de pions blancs et noirs que j’ai créé toutes les illustrations de go et de backgammon du livre « Jeux, Cultures et Stratégie » que j’ai publié chez Economica et dont il ne reste plus qu’une vingtaine d’exemplaires. Voici par exemple une belle position de début de partie :

Déplacement d’un objet dans Excel

Vous pouvez utiliser une multitude d’objets dans Excel... Certes, si l’on fait référence à la dimension « objet » du VBA, Excel dispose d’une grande variété d’objets, à chacun desquels on peut faire correspondre un code événementiel, selon que le curseur passe sur l’objet, qu’on lui fasse dessus un clic droit, un simple ou un double clic…

Les objets d’Excel pour le VBA, auxquels on peut associer un tel code, sont l’application Excel elle-même, le classeur, la feuille de calcul, un graphe, une image, une zone de texte, un groupe de cellules, une cellule, …

Dans l’article de ce jour, nous nous intéressons exclusivement aux objets que l’on peut loger dans une feuille de calcul Excel, par exemple un graphe, un objet de dessin, une image…

Supposons que, à l’aide de l’outil « Formes automatiques » de la barre d’outils « Dessin », puis de la commande « Formes de base », nous dessinions une ellipse :

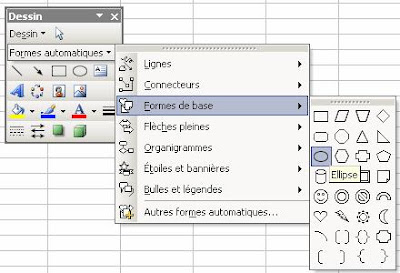Sachez alors que, lorsque vous dessinez la forme en traçant l’ellipse en question, plusieurs touches vous permettent d’atteindre des objectifs spécifiques :

● si vous faites un simple clic sur le curseur en forme de croix, vous tracez automatiquement une ellipse (un cercle par défaut) que vous pouvez redimensionner à loisir en utilisant n’importe laquelle de ses huit poignées ;

● si vous maintenez la touche [Maj] enfoncée lors du tracé de l’ellipse, celle-ci est toujours un cercle parfait ;

● si vous maintenez la touche [Alt] enfoncée lors du tracé de l’ellipse, celle-ci se définit toujours par rapport aux limites horizontale et verticale des cellules voisines ;

● si vous maintenez la touche [Ctrl] enfoncée lors du tracé de l’ellipse, vous maintenez fixe le centre de l’objet, alors que tous ses autres paramètres varient.

Remarque 1 – Nous aurions pu avoir accès plus rapidement à l’ellipse en cliquant directement dans son icône dans la commande de la première arborescence (copie d’écran ci-dessus), mais de passer par la commande
« Formes de base » nous a permis de vous montrer la variété des 24 formes ainsi proposées.

Remarque 2 – Les commentaires ci-dessus s’appliquent de la même façon aux autres objets. Ainsi, un rectangle tracé avec la touche [Maj] enfoncée est automatiquement un carré…

Remarque 3 – Les actions des commandes ci-dessus sont « cumulables » : si vous tracez une ellipse avec les touches [Maj] et [Ctrl] enfoncées, vous tracez des cercles concentriques…